The lecture “Quantum Computation and Error Correction” given by Dr. James Wootton introduced me to the fascinating (and very confusing) world of quantum computers. As my final project, I developed and evaluated a neural network that is able to perform a simple form of error correction.

Quantum Error Correction

A big issue for quantum computers is noise and its effect on qubits and their stored information. One way to achieve fault-tolerant quantum computing is by encoding one logical qubit with multiple physical ones. For instance, the surface code arranges physical qubits on a 2D lattice. This allows us to measure the syndrome, which a suitable decoding mechanism can use to diagnose which error likely occurred and then reverse it.

The Decodoku game has turned this decoding task in a fun puzzle game to help discover new decoding methods. For my project, I developed a decoder based on convolutional neural networks (CNN) that is able to play the game.

My CNN-Based Decoder

Using PyTorch, I trained and validated different network architectures until finally arriving at the following one:

Network Architecture

The decoding graph is represented as a matrix that is sent to the input layer. This is followed by:

• 6 hidden convolutional layers, each with 64 kernels of size 3
• a hidden fully connected layer with 512 nodes
• an output layer with k nodes, indicating the predicted error correction

As an activation function after each hidden layer the ReLU function is used.

Training Process

A big advantage of the problem setting is that we can generate an arbitrary amount of training data on the fly by simulating the introduction of errors. This has the additional benefit of eliminating the problem of overfitting our model: We do not have to make a distinction between training data and data for testing. It took around 50 epochs for the (cross-entropy) loss to converge, each with around 2 million unique generated training samples.

Results

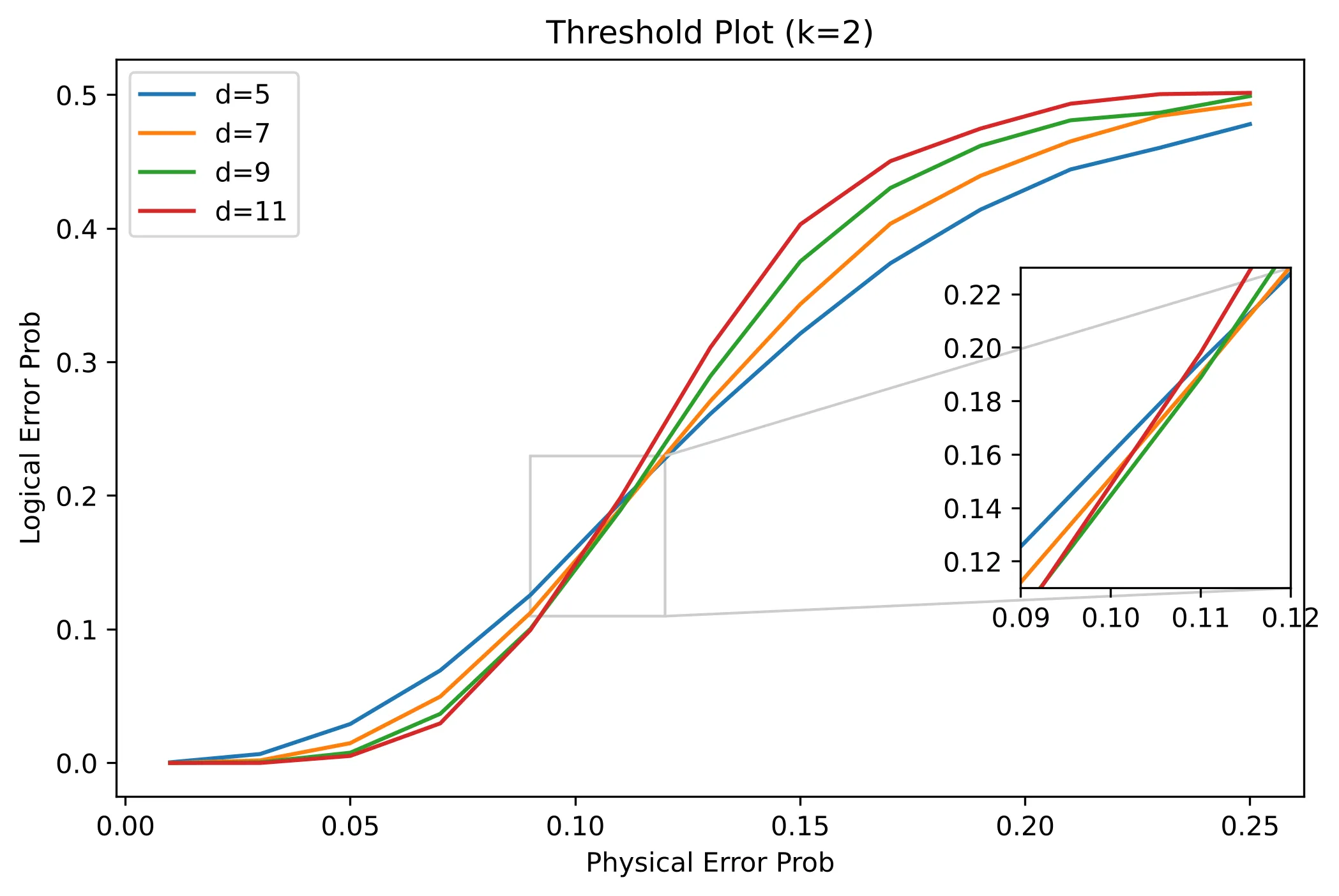
A threshold plot shows us the logical error probability after correcting for errors, given the physical error probability. Increasing d (and thus the number of physical qubits required to encode a single logical qubit) should ideally reduce the logical error probability. This is only possible to a certain threshold (the point where all the lines cross in the diagram). In the case of my decoder, this threshold is at p=0.11, a value that is quite good and comparable to established approaches like the Minimum Weight Perfect Matching (MWPM) decoder!

Error Correction for Qudits

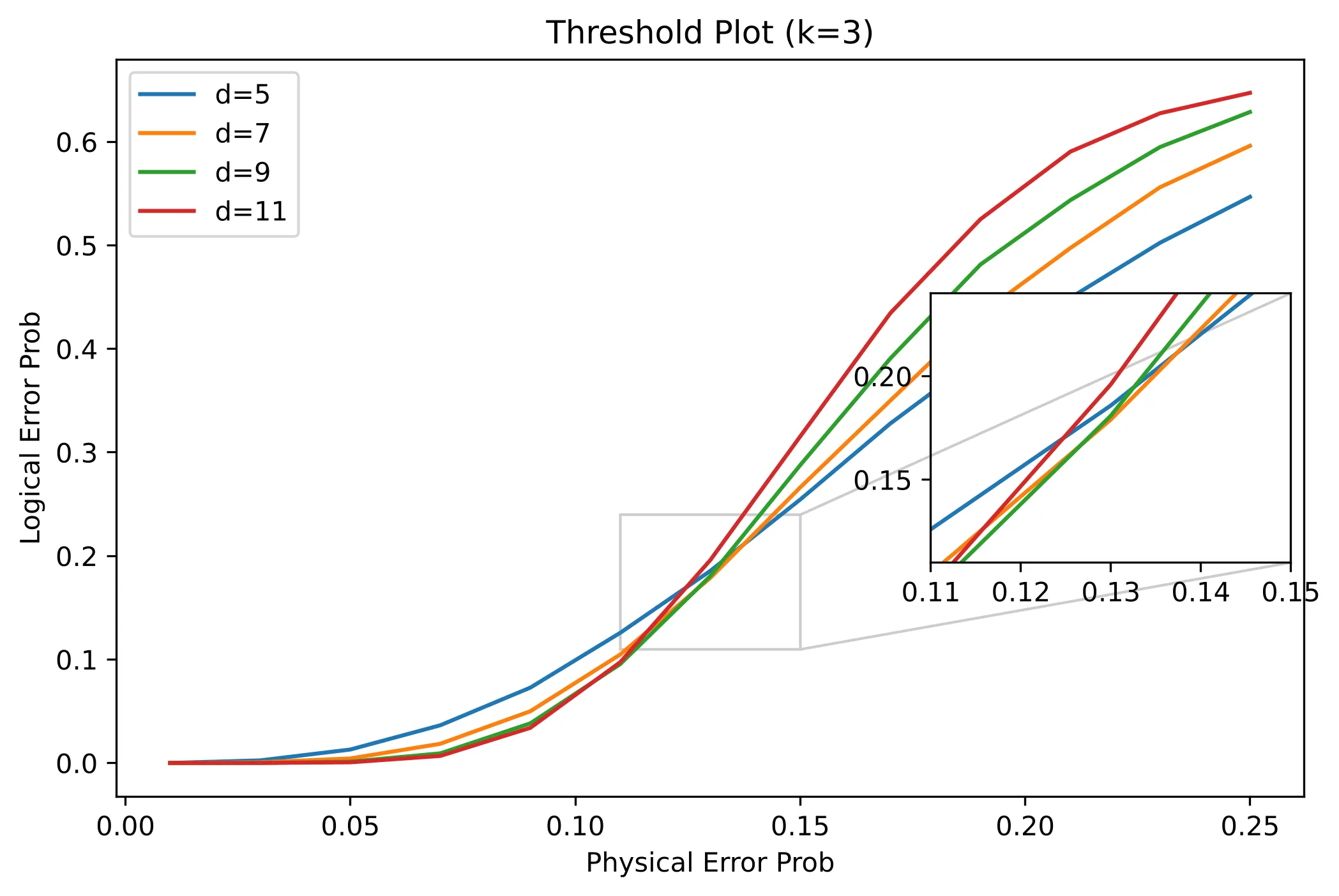
While a qubit represents the superposition of k=2 states, qudits generalize this concept to larger k. Unlike other common decoders like MWPM, this decoder can also be trained on systems with qudits that have k > 2. What makes them interesting, is their higher error-tolerance. This was also observed with the CNN-based decoder.

Links

• View the report that I wrote as part of the Quantum Computation lecture during my Master’s degree.
• A Medium article by Dr James Wootton on Quantum error correction (01.02.2023)
• SRF News Report on Decodoku (24.11.2016)